PPoS Dex
_______ _______ ______ ______
|_ __ \|_ __ \ .' ____ \ |_ _ `.
| |__) | | |__) | .--. | (___ \_| | | `. \ .---. _ __
| ___/ | ___// .'`\ \ _.____`. | | | |/ /__ \[ \ [ ]
_| |_ _| |_ | \__. || \____) | _| |_.' /| \__., > ' <
|_____| |_____| '.__.' \______.' |______.' '.__.'[__]`\_]
Algorand Pure Proof of Stake Decentralization Index (by cusma)
Algorand PPoS Decentralization Index
PPoS Dex is the Algorand Pure Proof of Stake (PPoS) Decentralization Index.
This project defines the index and provides a CLI tool to monitor it.
The monitoring tool is fully trustless: anyone can autonomulsy read the Algorand blockchain, do some client-side math, and publish the index on-chain.
Open index data are published daily by the PPoS Dex Oracle and then plotted as timeseries and snapshots.
PPoS Dex CLI provides also simple data analytics plots.
So, what "Decentralization Index" actually means?
DISCLAIMER
PPoS Dex has not been audited nor officially approved by the Algorand Foundation. This project is just a personal attempt to provide some metrics on Algorand's decentralization to the community. Algorand's decentralization is a common good, but will not happen by itself: the community as a whole should embrace the path towards the decentalization jointly with the Algorand Foundation, commiting to preserve it.
Introduction
Blockchain technology arose to fulfil the promise of genesis and exchange of digital native value in a disintermediated, censorship resistant, safe and scalable way.
Billions of people on the Earth (and maybe the Moon or Mars) would have the possibility of transacting without borders, barriers or discrimination within a distributed computational infrastructure that cancels out the need of trusted parties in between.
As well as exchange of digital information in the Internet era relies on Communication Protocols, the exchange of digital value relies on Consensus Protocols. Combining distributed computation, cryptography and game theory into a mathematical equilibrium Consensus Protocols are the engines that power blockchains, keeping the history of digital value unique, consistent, trustless, and tamper-proof within a distributed public ledger.
Blockchains' performances depend on their Consensus Protocols. At the beginning of this technological journey the so-called Proof of Work (PoW) consensus powered the first generation of Blockchains, with the merit of showing the existence of digital native value but at the same time facing the limitation of their own foundation.
In fact, running an interplanetary computational battle one against the other, just for the sake of validating the next block of data, takes a lot of time and enormous amount of energy. As "Proof of Work" suggests itself, showing off a commitment in the system, through the allocation of computational and energetic resources, is the core of this consensus mechanism.
However, Blockchains that run on PoW fail in fulfilling the promise of scalability, decentralisation, transaction speed, and costs, ending up relying on energey-intensive centralised computational farms.
The ultimate output of a Blockchain infrastrucuture is: reaching consensus to finalize state transitions of a distributed permissionless system in secure, scalable, and decentralized way.
The history of engineering teaches us that any technology evolves towards higher efficiency and scalability: who obtains the same useful output consuming less input resources and time survives.
Is PoW the only way to reach consensus and finalize a state transition of a distributed permissionless system in a secure way?
Is the foundational Blockchain promise doomed by the Buterin trilemma?
Here is where Algorand steps in.
Algorand Pure Proof of Stake Consensus
Prof. Silvio Micali combined state-of-art distributed computation, cryptography and game theory into the Algorand Pure Proof of Stake Consensus Protocol, to keep the foundational Blockchains' promise.
PPoS consensus is based on the Verifiable Random Function (VRF).
The VRF is used to create a fair, tamper-proof, secure and provable cryptographic sortition, in which people are free to take part as long as they own any amount of Algorand's native cryptocurrency, named ALGO.
Each "participating" ALGO acts as a ticket of a cryptographic lottery that secretly runs in parallel on Algorand network's nodes, for each new block, with minimal hardware requirements and neglectable energy consumption.
Users participating in Algorand PPoS do not delegate their votes, do not need a minimum stake to take part in the PPoS, and do not bond their ALGOs.
The cryptographic sortition is used to:
- Randomly and secretly elect a block proposer;
- Randomly and secretly elect a committee of validators for every proposed block.
Algorand PPoS solves Blockchains' trilemma acheiving at the same time:
- Scalability
- Security
- Decentralization
The point is: can we measure these properites?
Useful references:
Scalability
Scalability can be quantified in serveral ways:
- Block's finalization latency;
- Transactions per second;
- Transactions cost;
- Network power consumption;
- Node hardware requirements.
Algorand PPoS brings the number of finalized transactions per second from few dozen achieved by PoW up to 10k and shrinks transactions' finalization time form PoW’s dozen of minutes (or a few hours) to just 3.5 seconds, with no waste of energy, neglectable transaction’s cost (0.001 ALGO), and no hardware barriers.
So we have quantitative evidences of Algorand's scalability.
Security
Quantify security is not that simple (and out of the scope of this project).
PPoS is secure as soon as a supermajority of the stake is in non-malicious hands.
PPoS is provenly fork-less, ensuring blocks' instant finality.
Block proposer election and block validation remain secrets until accomplished, preventing malicious users to DDoS, corrupt or threat honest nodes.
Moreover, Algorand State Proofs secure Algorand's history with post-quantum resistant Falcon signatures.
A quantitative attestation of Algorand's security is represented by the fact that, at the time of writing (Sep 2023), Algorand never experienced a downtime nor a reorg since the genesis block (June 2019).
Decentralization
Defining a quantitative Decentralization Index for a Blockchain network running on Proof of Stake (PoS) consensus is not simple: a precise and rigorous definition of such a metric could easily fit as subject of an academic research (which is not the intent of this project).
So, how can we quantify PPoS decentralization?
Here is a proposal.
Consenus Protocol as Blockchain "engine"
To facilitate the presentation of our arguments for the definition of a Decentralization Index, let’s use an example that relies on the comparison of blockchain networks, running on PoS Consensus Protocols, with engines, exploring the concept of efficiency of a machine.
When mathematicians search for equations' solutions or when physicists do not know how to measure physical properties, they usually start investigating if such a solutions or properties have upper or lower bounds.
In 1842 the French physicist Nicolas Léonard Sadi Carnot discovered that the efficiency of any classical thermodynamic engine, that converts heat into work (or vice versa), must be lower than a theoretical upper bound represented by the efficiency of a purely ideal machine, named Carnot engine after him. Such a "perfect" engine is just a purely theoretical construct and cannot be built in practice.
This is probably the most elegant and general result in Classical Physics: it implies that any system undergoing any kind of thermodynamic cycle can only tend to the efficiency of a Carnot engine operating under the same conditions, never reach it, no matter how cleverly that system has been designed.
In the same way we try here to define an equivalent of a “Carnot engine” for PoS consensus decentralization.
Does such a theoretical decentralization upper bound even exist?
When should we say that a Blockchain running on PoS consensus is completely decentralized?
Decentralization factors
In order to reach a common understanding of what measuring decentralization even means, we should agree on some definitions.
We consider three different factors of decentralization that concur to define a Decentralization Index (\(DEX\)) of PoS networks:
- Nodes Hardware Decentralization (\(d_N\))
- Network Topology Decentralization (\(d_T\))
- Stake Decentralization (\(d_S\))
We have to quantify each of these three factors as bounded per-unit metrics so that the Decentralization Index can express "how far" a PoS Blockchain network is with respect to the “purely theoretical decentralization”.
The index can range from 0 (completely centralized) to 1 (completely decentralized):
\[ DEX = d_N \cdot d_T \cdot d_S \]
Let's try first to define an ideal theoretical condition of decentralization for each of those three per-unit factors. Then, everything deviating from those conditions will make a PoS Blockchain more real and far from platonic ideality.
Nodes Hardware Decentralization
The first factor for the evaluation of networks' decentralization is the rate of growth of the overall "nodes' hardware" connected to the network.
It is important to remark that this metric takes into account nodes' "growth rate" rather than just nodes' "absolute number", for the following reason: one could easily say that 10 nodes are better than 1 node, or that 100 nodes are better than 10 nodes. But, are 1.5 millions nodes really much better than 1 million nodes?
What we are trying to state here is that the number of nodes should be analyzed as a growth phenomenon, that tends to reach a steady state after which the addition of other nodes do not really impact decentralization in a linear and proportional way.
Sigmoid functions, like Logistic function or Error function, are a good way to model growth phenomena. Their characteristic S-shaped curve perfectly models a system, like a network, that exhibits a progression from small beginnings, that accelerates and approaches a climax over time.
Cumulative Distribution functions, similarly, contain information on a phenomenon regarding its growth or distribution before or after a certain "inflection point".
We propose to model the Nodes Hardware Decentralization as a Cumulative Distribution:
\[ d_{N} = 1 - e^{-\left(\frac{N}{\lambda}\right)^k} \]
that can theoretically range from 0 (no hardware growth) to 1 (complete hardware growth).
The parameters \(k\) and \(\lambda\) should be calibrated to best fit the growth phenomenon with respect to the growth "inflection point":
- \(k\) defines the speed of growth of the phenomenon;
- \(\lambda\) defines the order of magnitude of the inflection point for a given growth phenomenon.
How to tune \(\lambda\) for a Blockchain network could be debated around the following question:
What is the reasonable order of magnitude of nodes at which we can say that a Blockchain network has grown sufficiently?
Our opinion is that a meaningful decentralization "inflection point" for a Blockchain network should be greater than a few dozens or a few hundreds nodes. In particular, given the context of the analysis, we think adequate and reasonable to set:
- \(k = 2\) for the speed of growth;
- \(\lambda = 10^4\) for the inflection point magnitude.
\[ d_{N} = 1 - e^{-\left(\frac{N}{10^4}\right)^2} \]
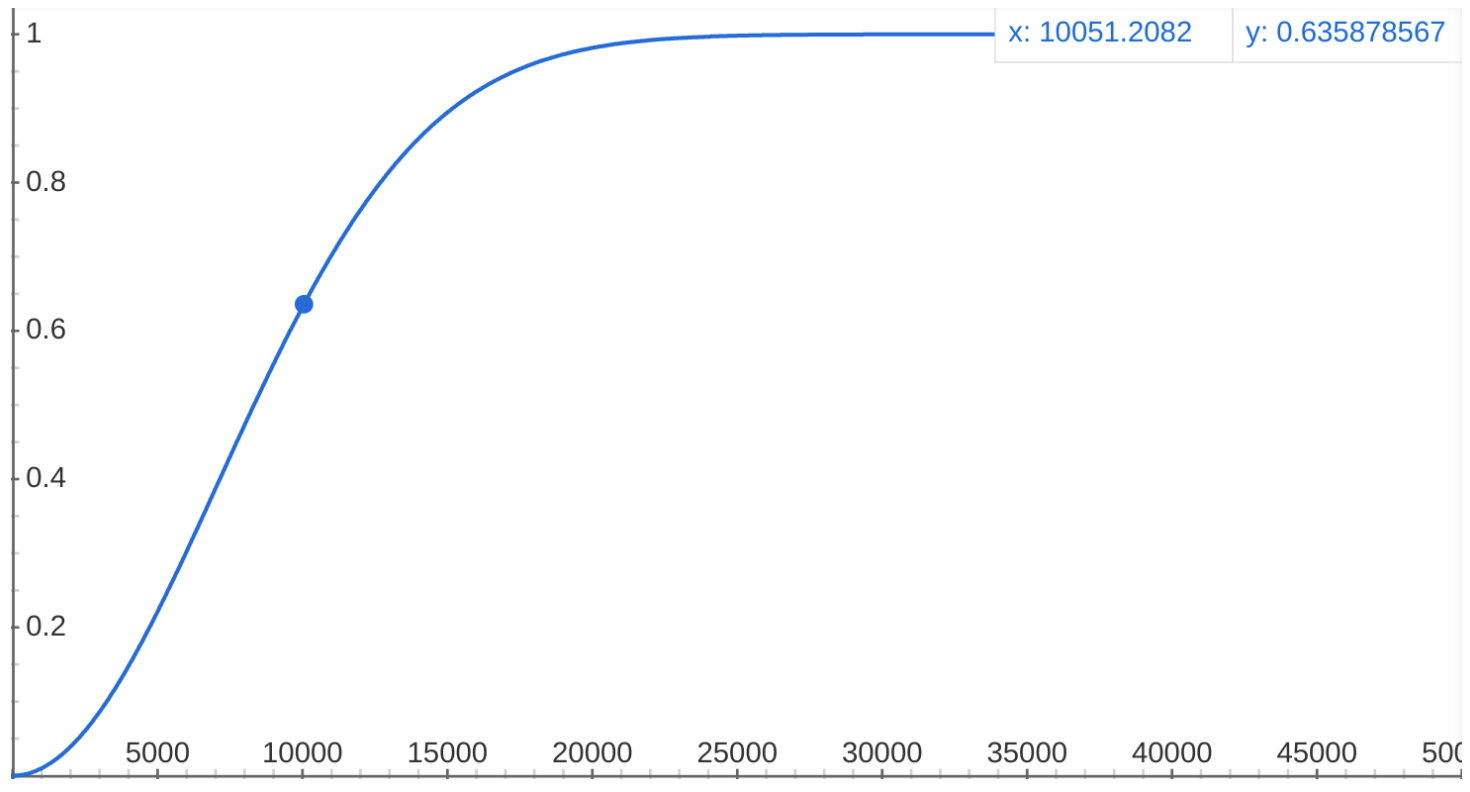
Since monitoring the number of connected validators nodes would require additional effort and resources, for the scope of this project we consider a perfect Nodes Hardware Decentralization (\( d_N = 1 \)), leaving the refinement of the calculation of this decentralization factor to future works.
Network Topology
Blockchain's public ledger is distributed across multiple nodes in a network. All these nodes work together, using the same set of software rules (the Consensus Protocol), to verify transactions that are eventually added to the finalized ledger.
In order to keep the state of such a distributed system unique, coherent and synchronized the information must flow across the network, ensuring efficient paths of communication between the nodes.
So, how nodes are connected to each other, forming a network, is the second relevant factor of decentralization, commonly known as Network Topology.
The message passing through the network can be achieved by routing the traffic with different techniques. In Algorand, at the time of writing (Sep 2023), information is spread across the network through “message gossiping” handled by the Relay Nodes. Relay Nodes route blocks to all connected nodes, finding highly efficient communication paths and reducing communication hops. Complementary fully P2P communications paths are under active research.
Paths of communication are therefore essential to ensure that no one is excluded from the communication: everybody should be able to talk and listen to each other without relying on a few dominant paths.
The more communication paths between nodes the more robust and decentralized the network.
Let’s try to visualize some communication paths examples between two generic nodes \(N_1\) and \(N_2\) connected through graphs that are intuitively different from each other:
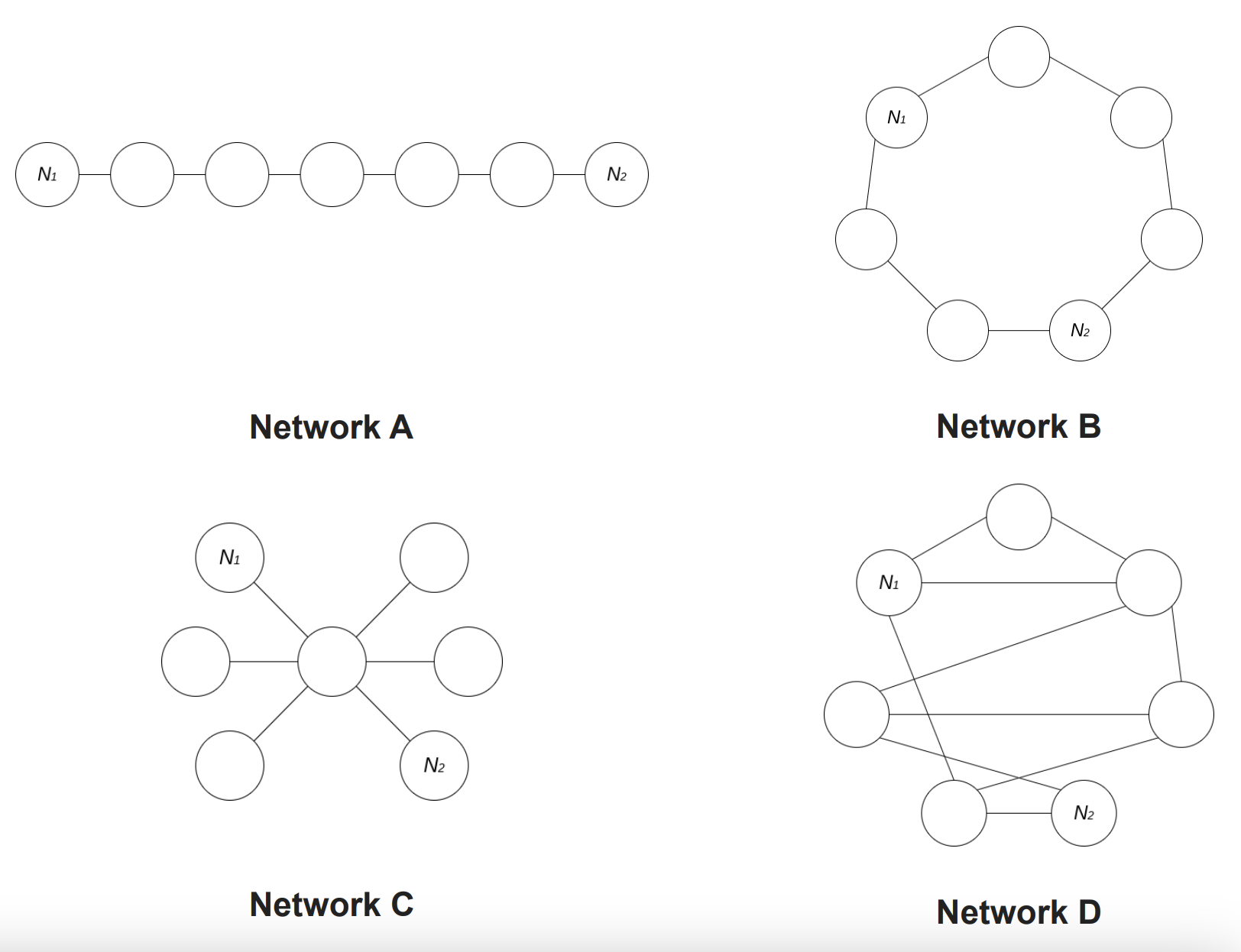
We can intuitively glimpse the difference between networks \(A\), \(B\), \(C\) and \(D\) with respect to the concept of “topology decentralization”. Graph \(D\) is intuitively “more decentralized” than graph \(A\), since it offers a larger set of communications paths between nodes \(N_1\) and \(N_2\).
Graph theory and network analysis define rigorous indicators of centrality, distribution and decentralization of a distributed system, assigning numbers or rankings to nodes within a graph corresponding to their network position.
Networks in which traffic is obliged to pass through a few dominant nodes, for example, are less “decentralized” than networks in which the traffic is free to flow through several possible communication paths.
Other metrics like Betweenness Centrality or Closeness Centrality are measures of centrality in a graph related to the evaluation of the shortest paths.
One possible metric that fits well our requirements for Network Topology Decentralization (being a per-unit metric bounded between 0 and 1) is the Central Point Dominance (\(CPD\)), which measures the maximum centrality of a node in a graph. This metric ranges from 0 to 1:
- 0 represents a network in which there is no node such that all shortest paths have to pass through it;
- 1 means all routes have to pass through that node.
Network \(C\) in the examples above, for instance, is a graph with Central Point Dominance equal to 1, since any message must pass through the central node to reach others.
In order to stay compliant with the rest of decentralization metrics used in this project (1 meaning maximum decentralization), we will consider the one's complement of the Central Point Dominance so:
\[ d_T = 1 - CPD \]
Network Topology Decentralization does not consider the degree of geo-delocalization of the physical infrastrucutre. More insights on this topic can be found here. For the scope of this project we consider a perfect Network Topology Decentralization (\( d_T = 1 \)), leaving the refinement of the calculation of this decentralization factor to future works.
Stake Decentralization
Since in PoS the probability of being elected as a block proposer or as a validator is directly proportional to validators' stakes, the distribution of such stake into the system is the last fundamental factor of PoS Blockchains decentralization.
We will say that the stake is "completely decentralized" (\(d_S = 1\)) if and only if:
- All the stake in circulation is participating in the PoS validation;
- All the validators participating in PoS validation hold the same amount of stake.
The first condition is quantified by the Stake Participation Index (\(S_P\)) while the second conditions is quantified by the Stake Inequality Index (\(S_I\)).
One could still argue that even if all the participating stake is equally distributed among validators, a PoS consenus could still be centralized due to the concentrarion of stake in a few accounts. So an additional Account Participation Index (\(A_P\)) is introduced.
Therefore:
\[ d_S = S_P \cdot S_I \cdot A_P \]
Stake Participation Index
The Stake Participation Index (\(S_P\)) measures stake participation rate in PoS validation. It can be quantified as:
\[ S_P = S_{dyn} \cdot S_{p}\]
Where:
- Stake Dynamics \(S_{dyn}\): is the fraction of ciruclating supply (\(S_c\)) over the genesis supply (\( S_g\)). It only applies to fixed genesis supply Blockchains;
- Stake Participation \(S_{p}\): is the fraction of validation supply (\(S_v\)) over the circulating supply (\( S_c\)).
\(S_P\) can theoretically range from 0 (no participation in PoS validation) to 1 (complete participation in PoS validation).
Stake Inequality Index
The Stake Inequality Index (\(S_I\)) measures validators' inequality. We can borrow from Macroeconomics well-known wealth inequality or concentration indexes, such as: the Gini Index, the Theil Indexes or the Herfindahl–Hirschman Index. Those indexes are indicators of concentration, used mainly to measure the degree of inequality in a society or the degree of competition in a given market.
Gini Index
Gini Index is a measure of statistical dispersion intended to represent the wealth inequality within a nation or any other group of people.
Given a stake distribution \(S\) over a set of \(N\) validators, the Simple Gini Index \(GI\) can be calculated as:
\[ GI(S) = \frac{2}{N} \frac{\sum_{i=1}^{N} i y_i}{\sum_{i=1}^{N} y_i} - \frac{N+1}{N} \]
where \( y_1 \le y_2 \le ... \le y_N\) are the sorted validators' stake.
\(GI\) can theoretically range from 0 (complete equality) to 1 (complete inequality), therefore it one’s complement \((1 - GI)\) is a good candidate for the \(DEX\) index.
Theil Indexes
Theil's Indexs, called Theil's L and Theil's T, measure the inequality of a stake distribution \(S\) over a set of \(N\) validators, with different sensitivities:
- Theil's L is more sensitive to differences at the lower end of the distribution (small stakes):
\[ T_L = \frac{1}{N} \sum_{i=1}^{N} \frac{y_i}{\mu} \ln{\left(\frac{y_i}{\mu} \right)} \]
- Theil's T is more sensitive to differences at the top of the distribution (large stakes):
\[ T_T = \frac{1}{N} \sum_{i=1}^{N} \ln{\left(\frac{\mu}{y_i}\right)} \]
where \(y_i\) is the validator's stake and \(\mu\) is the mean stake:
\[ \mu = \frac{1}{N} \sum_{i=1}^{N} y_i\]
Both \(T_L\) and \(T_T\) can theoretically range from 0 (complete equality) to \( +\infty \) (complete inequality) and represent two different evaluations of inequality, depending on what we tend to consider worse: having even a few small stakes among many large ones or having even a few large stakes among many small ones.
Theil’s Indexes are not upper bounded, so are not good candidates for the \(DEX\) index. For sake of completeness we will evaluate them separately.
Herfindahl–Hirschman Index
Herfindahl–Hirschman Index is another indicator of concentration, mainly used to measure the degree of competition in a given market.
Given a stake distribution \(S\) over a set of \(N\) validators, the \(HHI\) index can be calculated as:
\[ HHI(S) = \sum_{i=1}^{N} {s_i}^2 \]
where \(s_i\) is the stake share of validator \(i\) in the total validating stake \(S\).
\(HHI\) can theoretically range from 0 (perfectly competitive market) to 1 (monopoly), therefore it one’s complement \((1 - HHI)\) is a good candidate for the \(DEX\) index.
The \(HHI\) implicitly considers both the stake distribution among the validators accounts and the absolute number of validators accounts. Therefore, in order to avoid double counting of the account participation factor, \(A_P = 1\) when \(S_I = 1 - HHI\).
Example 1
The largest validator holds 80% of the stake, the next 5 largest validators hold 2% each, the reminder is equally distributed among 10 validators:
\[ HHI = {0.80}^2 + 5 \cdot {0.02}^2 + 10 \cdot {0.01}^2 = 0.643 \]
Example 2
The 6 largest validators hold 15% of the stake each, the reminder is equally distributed among 10 validators:
\[ HHI = 6 \cdot {0.15}^2 + 10 \cdot {0.01}^2 = 0.136 \]
Example 3
All the stake is equally distributed among 20 validators:
\[ HHI = 20 \cdot {0.05}^2 = 0.005 \]
Example 4
All the stake is equally distributed among 100 validators:
\[ HHI = 100 \cdot {0.01}^2 = 0.001 \]
Account Participation Index
The Account Participation Index (\(A_P\)) represents the fraction of validator accounts (\(A_v\)) over the total accounts (\( A_{tot}\)):
\[ A_P = \frac{A_v}{A_{tot}} \]
It can theoretically range from 0 (no account participating in PoS validation) to 1 (all existing accounts participating in PoS validation).
In account-based Blockchains (like Algorand), accounts are identified by public keys. Permissionless and public networks are pseudonymous by design, therefore there is no way to assert if different public keys belong to different users. We assume that each public key belongs to a different participant in the PPoS consensus, with their own skin in the game.
Pure Proof of Stake Decentralization Index
We finally apply the \(DEX\) index to Algorand’s PPoS, defining the \(PPoS DEX\) index.
Given the \(DEX\) index definition, we say Algorand PPoS is "completely decentralized" iff:
- Algorand Nodes Hardware is completely decentralized (\(d_N = 1\));
- Algorand Network Topology is completely decentralized (\(d_T = 1\));
- Algorand Validating Stake is completely decentralized (\(d_S = 1\)).
As pointed out in previous chapters, due to resource and time constraints, we assume complete decentralization both for Nodes Hardware and Network Topology, leaving the refinement of these assumptions to future works (community contributions are welcome).
The ALGO has a total supply of 10B, hardcoded in the genesis block, so the Stake Dynamics applies to ALGO.
We say Algorand Validating Stake is “completely decentralized” iff:
- All the ALGO genesis supply is circulating in the ecosystem (\(S_{dyn}\));
- All the ALGO circulating supply is taking part to the PPoS (\(S_{prt}\));
- All the accounts that owns ALGOs are taking part to PPoS (\(A_{prt}\));
- All the accounts participating in PPoS hold the same amount of ALGO (\(GI\) or \(HHI\));
Combining the 4 points above, we know "how far" PPoS is from its purely theoretical decentralization, being aware that the PPoS only tends to the ideal condition, never reaching it.
PPoS DEX v1
\[ PPoS DEX = d_N \cdot d_T \cdot S_{dyn} \cdot S_{prt} \cdot A_{prt} \cdot (1 - GI(S)) \]
PPoS DEX v2
\[ PPoS DEX = d_N \cdot d_T \cdot S_{dyn} \cdot S_{prt} \cdot (1 - HHI(S)) \]
Metrics summary
| METRIC | SYMBOL | DESCRIPTION |
|---|---|---|
| ALGO Dynamics | \(S_{dyn}\) | 0 = no ALGO circulation, 1 = complete ALGO circulation |
| ALGO Participation | \(S_{prt}\) | 0 = no PPoS participation, 1 = complete PPoS participation |
| Accounts Participation | \(A_{prt}\) | 0 = no PPoS accounts participation, 1 = complete PPoS accounts participation |
| ALGO HHI | \(1 - HHI(A)\) | Considers all ALGO stakes, whether they participate in the PPoS or not |
| PPoS Gini | \(1 - GI(S)\) | PPoS staking inequality, regardless the number of participating accounts |
| PPoS Theil’L | \(TL(S)\) | PPoS staking inequality, sensitive to differences at the lower end of the distribution (small stakes) |
| PPoS Theil’T | \(TT(S)\) | PPoS staking inequality, sensitive to differences at the high end of the distribution (large stakes) |
| PPoS HHI | \(1 - HHI(S)\) | PPoS staking inequality, takes the number of participating accounts in consideration |
Minimum balance filter
Due to the huge number of accounts already existing on Algorand (more than 30M at the time of writing, Sep 2023), fetching and processing all of them would be computationally heavy and resource demaning for this project. Therefore, PPoS Dex CLI applies an optional "minimum balance filter", to ignore accounts with balances lower than a threshold (default 1000 ALGO). Such a filtering operation has a noise-canceling effect that makes the data retrieval and procces lighter, without compromising data statistical significancy of the indexes.
PPoS Timeseries
ALGO Dynamics

Accounts Participation

ALGO Inequality

PPoS Inequality (Bounded)

PPoS Inequality (Unbounded)

PPoS Dex

PPoS Snapshot
ALGO Dynamics

Accounts Participation

PPoS Inequality

PPoS Dex

PPoS Dex CLI
PPoS Dex CLI provides the following utilities:
- Publishing PPoS Dex data point;
- Monitoring PPoS Dex trend (timeseries);
- Monitoring PPoS Dex latest state (snapshot);
- Exporting PPoS Dex data to
.csvfor external analysis.
Install
PPoS Dex uses Poetry for dependencies management.
Clone PPoS Dex repository, cd into it,
and:
poetry install
You are all set!
Node setup
PPoS Dex interacts both with Algorand Node and an Indexer. You may choose:
- Your local hosted Node and Indexer (e.g. AlgoKit);
- A third party Node and Indexer APIs.
PPoS Dex uses AlgoNode APIs by default.
If you prefer using your local hosted Node and Indexer (or other API providers), the following environment variables must be set:
export ALGOD_SERVER=...
export ALGOD_TOKEN=...
export INDEXER_SERVER=...
export INDEXER_TOKEN=...
Usage
Intreacting with PPoS Dex CLI is pretty easy, just ask for help:
$ poetry run python3 ppos_dex.py --help
Algorand PPoS Decentralization Index.
Usage:
ppos_dex.py publish [--algo-threshold=<a>] [--localhost | --test]
ppos_dex.py timeseries [--publisher=<p>] [--algo-threshold=<a>] [--start-block=<s>] [--end-block=<e>] [--localhost | --test] [--save]
ppos_dex.py snapshot [--publisher=<p>] [--algo-threshold=<a>] [--start-block=<s>] [--end-block=<e>] [--localhost | --test] [--save]
ppos_dex.py export [--publisher=<p>] [--algo-threshold=<a>] [--start-block=<s>] [--end-block=<e>] [--localhost | --test]
ppos_dex.py health [--localhost | --test]
ppos_dex.py [--help]
Commands:
publish Publish PPoS Dex data. Requires ALGO_MNEMONIC environment variable.
timeseries Plot PPoS Dex timeseries.
snapshot Plot latest PPoS Dex data point.
export Export PPoS Dex data to `.csv`.
health Check Algod and Indexer status.
Options:
-a, --algo-threshold=<a> [default: 1000]
-p, --publisher=<p> [default: WIPE4JSUWLXKZZK6GJ6VI32PX6ZWPKBRH5YFRJCHWOVC73P5RI4DGUQUWQ]
-s, --start-block=<s> [default: 11476070]
-e, --end-block=<e>
-l, --localhost
-t, --test
-h, --help
Use the health command to check Algorand Nods and Indexer availability:
poetry run ppos_dex.py health [--localhost | --test]
Publish PPoS Dex data points
Contribute publishing trustless PPos Dex data points on Algorand blockchain paying just the minimum transaction fee (currently 0.001 ALGO).
Set your publisher mnemonic as environment variable:
export ALGO_MNEMONIC=...
and use the publish command:
$ poetry run python3 ppos_dex.py publish [--algo-threshold=<a>] [--localhost | --test]
📈 PPoS Dex published data:
{
"algo_threshold": 1000,
"accounts": 13346,
"algo_dynamics": 0.3741854092978301,
"ppos_online_stake": 0.598241416943984,
"ppos_online_accounts": 0.01715869923572606,
"ppos_gini": 0.829793933948626,
"ppos_theil_l": 4.640220128476622,
"ppos_theil_t": 1.5593480873810057,
"ppos_dex": 0.0006537665878508702,
"timestamp": "2021-01-06 00:22:09.607573"
}
Options
[--algo-threshold=<at>]consider only accounts that own more than this threshold (default: 1000 ALGO);[--localhost | test]select local hosted Node and Indexer / other API providers, or default TestNet end-points.
Is worth noting that lower values of [--algo-threshold=<at>] will require more
querying efforts. You should avoid lowering the default threshold, expecially if
you are using third party API services.
Plot PPoS Dex timeseries
Plot PPoS Dex timeseries published to evaluate trends.
potery run ppos_dex.py timeseries [--publisher=<p>] [--algo-threshold=<a>] [--start-block=<s>] [--end-block=<e>] [--localhost | --test] [--save]
Options
[--publisher=<p>]publisher account address (default: PPoS Dex Oracle account);[--algo-threshold=<t>]plot only data of accounts that own more than this threshold (default: 1000 ALGO);[--start-block=<s>]plot data from this block (if availables);[--end-block=<e>]plot data until this block;[--localhost | test]select local hosted Node and Indexer / other API providers, or default TestNet end-points;[--save]save plots in./docs/images/timeseries.
Plot PPoS Dex snapshot
Take a snapshot of latest published PPoS Dex data.
poetry run ppos_dex.py snapshot [--publisher=<p>] [--algo-threshold=<a>] [--start-block=<s>] [--localhost | --test] [--save]
Options
[--publisher=<p>]publisher account address (default: PPoS Dex Oracle account);[--algo-threshold=<t>]plot only data of accounts that own more than this threshold (default: 1000 ALGO);[--start-block=<s>]plot data from this block (if availables);[--localhost | test]select local hosted Node and Indexer / other API providers, or default TestNet end-points;[--save]save plots in./docs/images/snapshot.
Export Plot PPoS Dex data
Export PPoS Dex data to csv file for external analysis.
poetry run ppos_dex.py export [--publisher=<p>] [--algo-threshold=<a>] [--start-block=<s>] [--end-block=<e>] [--localhost | --test]
Options
[--publisher=<p>]publisher account address (default: PPoS Dex Oracle account);[--algo-threshold=<t>]export only data of accounts that own more than this threshold (default: 1000 ALGO);[--start-block=<s>]export data from this block (if availables);[--end-block=<e>]export data until this block;[--localhost | test]select local hosted Node and Indexer / other API providers, or default TestNet end-points.
Contribute
PPoS Dex project is open source, community contributions are welcome!
If you find PPoS Dex a good and useful tool please consider tipping the PPoS Dex Oracle account to support transaction fees:
WIPE4JSUWLXKZZK6GJ6VI32PX6ZWPKBRH5YFRJCHWOVC73P5RI4DGUQUWQ
Contributors
- manuelmauro (for letting me discover
mdBook)