Nodes Hardware Decentralization
The first factor for the evaluation of networks' decentralization is the rate of growth of the overall "nodes' hardware" connected to the network.
It is important to remark that this metric takes into account nodes' "growth rate" rather than just nodes' "absolute number", for the following reason: one could easily say that 10 nodes are better than 1 node, or that 100 nodes are better than 10 nodes. But, are 1.5 millions nodes really much better than 1 million nodes?
What we are trying to state here is that the number of nodes should be analyzed as a growth phenomenon, that tends to reach a steady state after which the addition of other nodes do not really impact decentralization in a linear and proportional way.
Sigmoid functions, like Logistic function or Error function, are a good way to model growth phenomena. Their characteristic S-shaped curve perfectly models a system, like a network, that exhibits a progression from small beginnings, that accelerates and approaches a climax over time.
Cumulative Distribution functions, similarly, contain information on a phenomenon regarding its growth or distribution before or after a certain "inflection point".
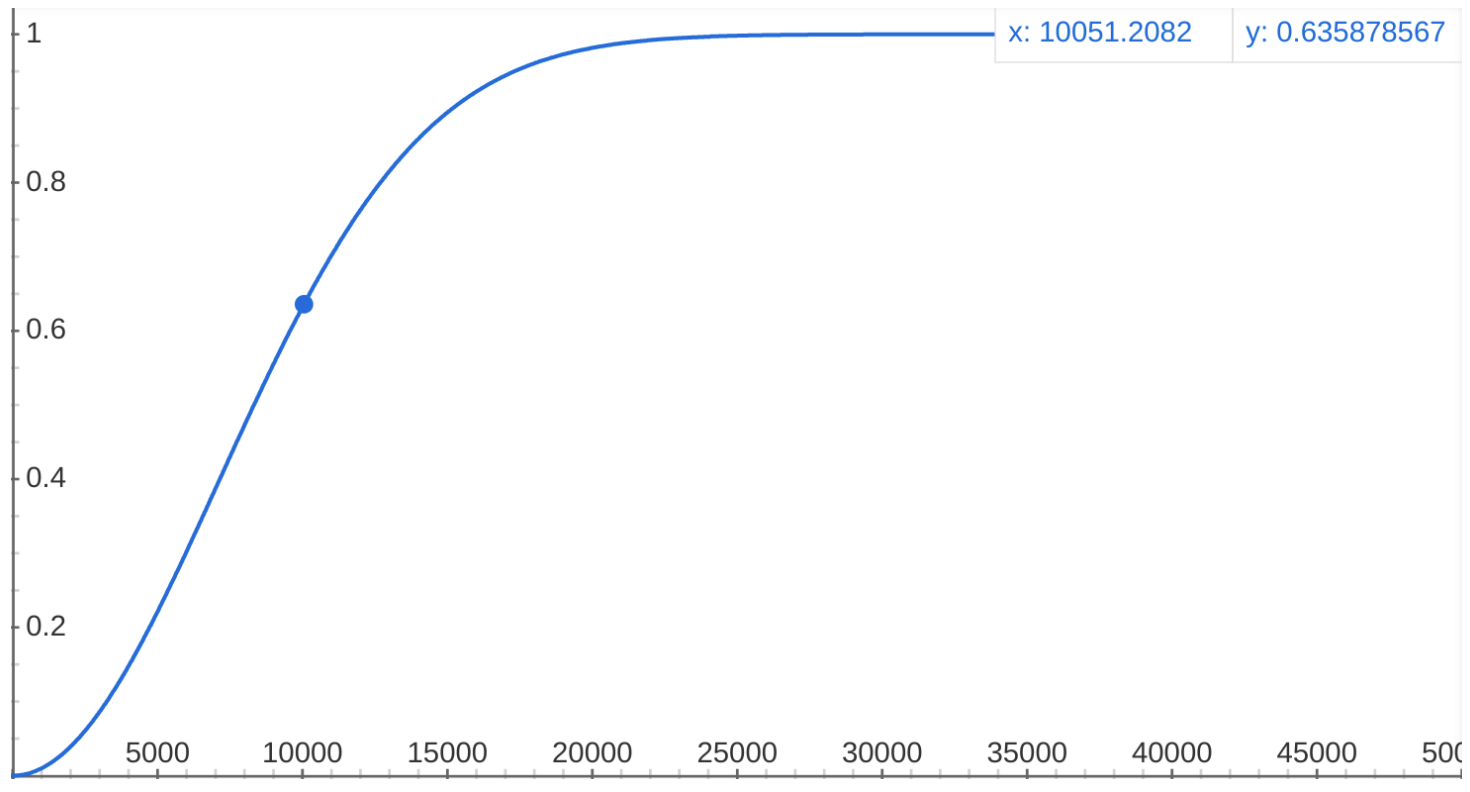
We propose to model the Nodes Hardware Decentralization as a Cumulative Distribution:
\[ d_{N} = 1 - e^{-\left(\frac{N}{\lambda}\right)^k} \]
that can theoretically range from 0 (no hardware growth) to 1 (complete hardware growth).
The parameters \(k\) and \(\lambda\) should be calibrated to best fit the growth phenomenon with respect to the growth "inflection point":
- \(k\) defines the speed of growth of the phenomenon;
- \(\lambda\) defines the order of magnitude of the inflection point for a given growth phenomenon.
How to tune \(\lambda\) for a Blockchain network could be debated around the following question:
What is the reasonable order of magnitude of nodes at which we can say that a Blockchain network has grown sufficiently?
Our opinion is that a meaningful decentralization "inflection point" for a Blockchain network should be greater than a few dozens or a few hundreds nodes. In particular, given the context of the analysis, we think adequate and reasonable to set:
- \(k = 2\) for the speed of growth;
- \(\lambda = 10^4\) for the inflection point magnitude.
\[ d_{N} = 1 - e^{-\left(\frac{N}{10^4}\right)^2} \]
Since monitoring the number of connected validators nodes would require additional effort and resources, for the scope of this project we consider a perfect Nodes Hardware Decentralization (\( d_N = 1 \)), leaving the refinement of the calculation of this decentralization factor to future works.