Network Topology
Blockchain's public ledger is distributed across multiple nodes in a network. All these nodes work together, using the same set of software rules (the Consensus Protocol), to verify transactions that are eventually added to the finalized ledger.
In order to keep the state of such a distributed system unique, coherent and synchronized the information must flow across the network, ensuring efficient paths of communication between the nodes.
So, how nodes are connected to each other, forming a network, is the second relevant factor of decentralization, commonly known as Network Topology.
The message passing through the network can be achieved by routing the traffic with different techniques. In Algorand, at the time of writing (Sep 2023), information is spread across the network through “message gossiping” handled by the Relay Nodes. Relay Nodes route blocks to all connected nodes, finding highly efficient communication paths and reducing communication hops. Complementary fully P2P communications paths are under active research.
Paths of communication are therefore essential to ensure that no one is excluded from the communication: everybody should be able to talk and listen to each other without relying on a few dominant paths.
The more communication paths between nodes the more robust and decentralized the network.
Let’s try to visualize some communication paths examples between two generic nodes \(N_1\) and \(N_2\) connected through graphs that are intuitively different from each other:
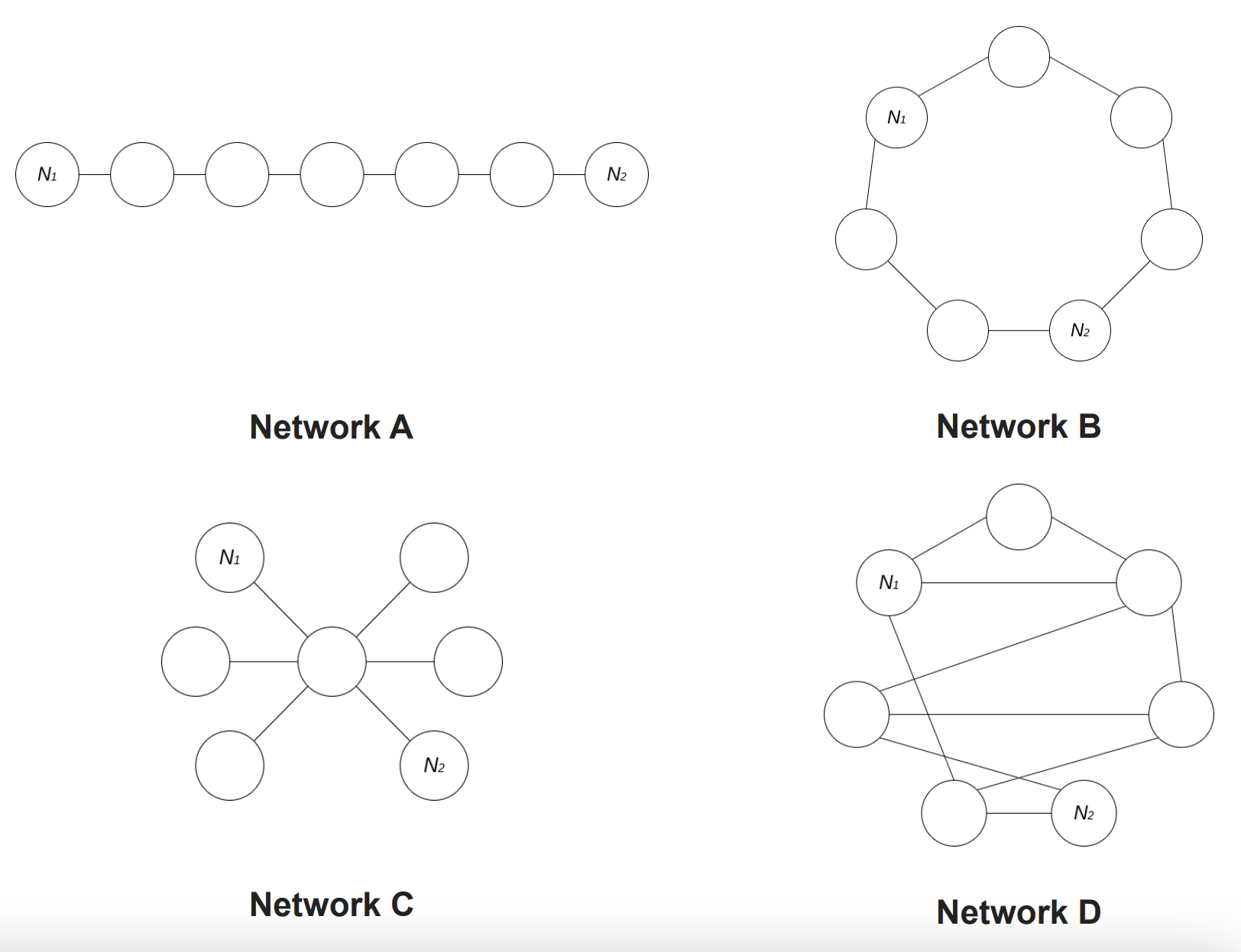
We can intuitively glimpse the difference between networks \(A\), \(B\), \(C\) and \(D\) with respect to the concept of “topology decentralization”. Graph \(D\) is intuitively “more decentralized” than graph \(A\), since it offers a larger set of communications paths between nodes \(N_1\) and \(N_2\).
Graph theory and network analysis define rigorous indicators of centrality, distribution and decentralization of a distributed system, assigning numbers or rankings to nodes within a graph corresponding to their network position.
Networks in which traffic is obliged to pass through a few dominant nodes, for example, are less “decentralized” than networks in which the traffic is free to flow through several possible communication paths.
Other metrics like Betweenness Centrality or Closeness Centrality are measures of centrality in a graph related to the evaluation of the shortest paths.
One possible metric that fits well our requirements for Network Topology Decentralization (being a per-unit metric bounded between 0 and 1) is the Central Point Dominance (\(CPD\)), which measures the maximum centrality of a node in a graph. This metric ranges from 0 to 1:
- 0 represents a network in which there is no node such that all shortest paths have to pass through it;
- 1 means all routes have to pass through that node.
Network \(C\) in the examples above, for instance, is a graph with Central Point Dominance equal to 1, since any message must pass through the central node to reach others.
In order to stay compliant with the rest of decentralization metrics used in this project (1 meaning maximum decentralization), we will consider the one's complement of the Central Point Dominance so:
\[ d_T = 1 - CPD \]
Network Topology Decentralization does not consider the degree of geo-delocalization of the physical infrastrucutre. More insights on this topic can be found here. For the scope of this project we consider a perfect Network Topology Decentralization (\( d_T = 1 \)), leaving the refinement of the calculation of this decentralization factor to future works.